Pacing a climb with varying gradients

It’s hill climb season and that means our inboxes are full of pacing questions. Most of these questions come from pacing climbs with varying gradients. Everyone knows how to pace a climb that’s a steady gradient – just figure out roughly how hard to go then go that hard. With variations in gradient however, things change. Other forces come into play, many climbs have a flat bit at the bottom and gradually get steeper, others are stepped climbs or may even contain a small descent in the middle. The thing is, with any climb of varying gradient, pacing it evenly is likely not the fastest way to get up it with whatever available energy you have at your disposal. To explain this concept we will jump straight into an example… 


A climb with an increasing slope… 

Let’s imagine an example where we have a climb with a gradient that increases slowly from flat to completely vertical. At any point on the climb, the forces acting on something ascending this climb (in our case, usually a bike) are… 

Yes, we’ve ignored air resistance as this complicates matters. While the physics engine that myWindsock runs on can handle this complication, for now we will make some kind of low speed assumption that allows us to ignore air resistance (though a good rule of thumb is that it becomes more important to think about in hill climbs the faster you go). 


The thing for us that’s important is the component of weight acting down the slope – this is the weight that we feel when trying to accelerate the bike up the climb. This component of weight is proportional to the sin of the slope angle. How does the component of weight acting change as that angle increases?

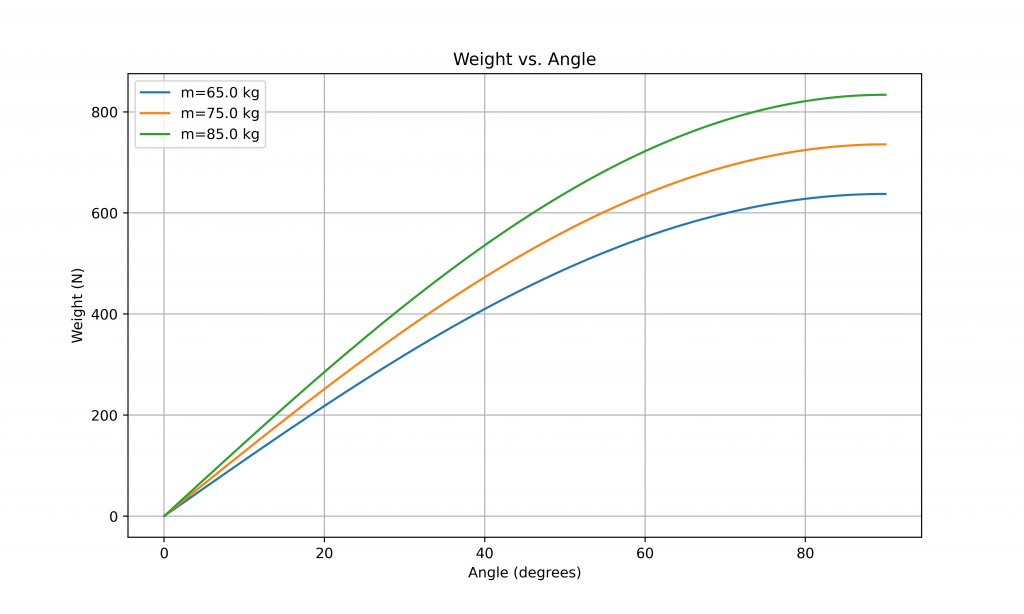
Here we have a plot of the force experienced by a rider due to their weight (with other components of resistance ignored) as the angle of a climb increases. Three system masses are included here to show how these differences are felt on riders with differing masses. The y-axis, labelled “Weight”, shows us the effective weight felt. The angle here goes from zero (completely flat) to 90 degrees (think literal vertical wall). In reality, a 20% gradient is only 11 degrees but the larger angles are shown to emphasise the point. At these lower angles, the proportion of force can be assumed to be linear (at small angles sin(x) is roughly equal to x).

How should I pace then?

Over any given duration, you’ll have some given energy budget (ie, you know can normalise some power for some duration) and this should be your starting point. From here, it’s about thinking where to invest that energy for the biggest return on speed. Generally speaking, this equates to going harder on steep bits as the resistive forces increase with speed at a slower rate when you’re moving slower (due to the exponents in the aerodynamic equation).

In simple language, practical advice would be to change what you’re thinking about based on speed – for flat parts you’re working against air resistance, for moderate you’re working against both air and gravity and for steep you’re working primarily against gravity. Go harder on steep bits, get more aero on flat bits.

Thinking about, and quantifying, these things is far from simple and it’s made easier when you have a physics engine to handle the calculations for you meaning you can focus entirely on preparing yourself for race day – knowing that you’ve used all available data to inform a race plan you can be confident in. If that sounds like your sort of thing – sign up to myWindsock today.